Cálculo Diferencial
lunes, 29 de marzo de 2021
lunes, 8 de marzo de 2021
PARCIAL 02: Ejercicios guiados
Aqui se muestra una serie de videos con ejerciicos guiados para su realizacion en su libreta de apuntes.
PARCIAL 01: Funciones
Funciones
Una función (f) es una relación entre un conjunto dado X (llamado dominio) y otro conjunto de elementos Y (llamado codominio) de forma que a cada elemento x del dominio le corresponde un único elemento f(x) del codominio (los que forman el recorrido, rango o ámbito).
De manera más simple: Una función es una relación entre dos magnitudes, de tal manera que a cada valor de la primera corresponde un único valor de la segunda.
La función se puede ilustrar mediante un diagrama usando flechas para indicar la forma en que se asocian los elementos de los dos conjuntos.
Básicamente, hay tres formas para expresar una función: mediante una tabla de valores (como el ejemplo anterior), mediante una expresión algebraica o, como veremos luego, mediante una gráfica.
Tipos de funciones
Dependiendo de ciertas características que tome la expresión algebraica o notación de la función f en x, tendremos distintos tipos de funciones:
Función constante
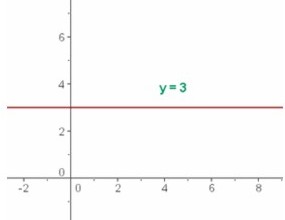
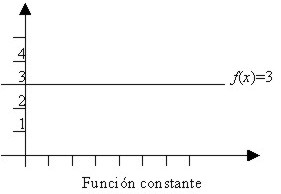
Una función de la forma f(x) = b, donde b es una constante, se conoce como una función constante.
Por ejemplo, f(x) = 3, (que corresponde al valor de y) donde el dominio es el conjunto de los números reales y el recorrido es {3}, por tanto y = 3. La gráfica de abajo muestra que es una recta horizontal.
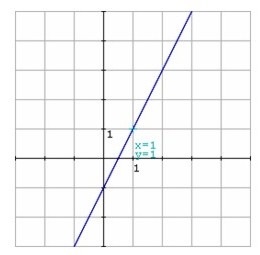
Función lineal
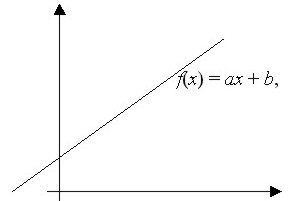
Una función de la forma f(x) = mx + b se conoce como una función lineal, donde m representa la pendiente y b representa el intercepto en y. La representación gráfica de una función lineal es una recta. Las funciones lineales son funciones polinómicas.
Ejemplo:
F(x) = 2x - 1
Es una función lineal con pendiente m = 2 e intercepto en y en (0, -1). Su gráfica es una recta ascendente.
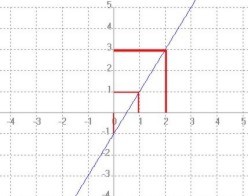
Para trazar la gráfica de una función lineal solo es necesario conocer dos de sus puntos.
La ecuación matemática que representa a esta función, como ya vimos, es f(x) = ax + b, donde f(x) corresponde al valor de y, entonces
y = ax + b
Donde "a" es la pendiente de la recta, y "b" es la ordenada al origen.
La pendiente indica la inclinación de la recta, cuanto sube o baja y cuanto avanza o retrocede. Esto depende del signo que tenga.
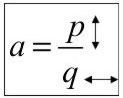
El valor de "a" siempre es una fracción (si no tiene nada abajo, es porque tiene un 1), donde el numerador (p) me indica cuanto sube o baja, y el denominador (q) indica cuanto avanzo o retrocedo.
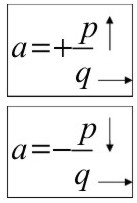
Aprendido esto, y según el signo de la fracción, la pendiente se marca de la siguiente forma:
La ordenada al origen (b) es el valor donde la recta corta al eje y.
La recta siempre va a pasar por el punto (0; b)
Representación gráfica de una función lineal o función afín
Para graficar una recta, alcanza con los datos que da la ecuación matemática de la función, y se opera de la siguiente manera:
1. Se marca sobre el eje y la ordenada al origen, el punto por donde la recta va a cortar dicho eje.
2. Desde ese punto, subo o bajo según sea el valor de "p" y avanzo o retrocedo según indique el valor de "q". En ese nuevo lugar, marco el segundo punto de la recta.
3. Se podría seguir marcando puntos con la misma pendiente, pero con 2 de ellos ya es suficiente como para poder graficar la recta.
4. Teniendo ya los dos puntos, con regla se traza la recta que pasa por los mismos.
Ejemplo:
Graficar la siguiente función:
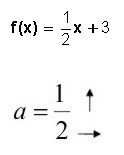
La ordenada al origen (3) me indica que me debo parar sobre el eje y en el 3.
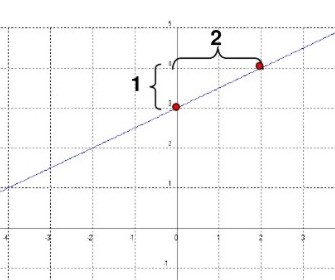
También podemos graficar una función dando valores a x y obteniendo dos puntos en las coordenadas.
Ejemplo:
Graficar la función dada por f(x) = 2x – 1
Solución
Como la función es lineal se buscan dos puntos de la recta; para ello, se le dan valores a x y se encuentran sus imágenes respectivas, esto es:
Si x = 0, se tiene que f (0) = 2(0) – 1 = - 1
Si x = 2, se tiene que f (2) = 2(2) – 1 = 3
Así, los puntos obtenidos son (0, -1) y (2, 3), por los cuales se traza la gráfica correspondiente.
|
Función polinómica

El dominio de todas estas funciones polinómicas es el conjunto de los números reales (porque el elemento x puede ser cualquier número real).
Función cuadrática
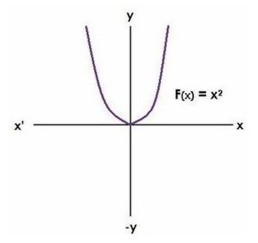
Una función de la forma f(x) = ax2 + bx + c, donde a, b y c son constantes y a es diferente de cero, se conoce como una función cuadrática.
La representación gráfica de una función cuadrática es una parábola. Una parábola abre hacia arriba si a > 0 y abre hacia abajo si a < 0. El vértice de una parábola se determina por la fórmula:
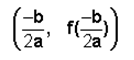
Las funciones cuadráticas son funciones polinómicas.
Ejemplo:
|
F(x) = x2 representa una parábola que abre hacia arriba con vértice en (0,0). |
Función racional
Una función racional es el cociente de dos funciones polinómicas. Así es que q es una función racional si para todo x en el dominio, se tiene:

Nota: El dominio de una función polinómica son los números reales; sin embargo, el dominio de una función racional consiste de todos los números reales excepto los ceros del polinomio en el denominador (ya que la división por cero no está definida).
Función de potencia
Una función de potencia es toda función de la forma f(x) = xr, donde r es cualquier número real.
Las funciones f(x) = x4/3 y h(x) = 5x3/2 son funciones de potencia.
Ejercicios y ejemplos con funciones en general:
Expresar mediante una fórmula la función que asocia a cada número:
a) Su cuádruplo.
La función es: f (x) = 4x.
b) Un número 2 unidades mayor.
La función es: f (x) = x + 2.
c) Su mitad menos 1.
La función es: f (x) = x/2 - 1.
d) El cuadrado del número que es una unidad menor.
La función es: f (x) = (x - 1)2
Veamos algunos otros ejemplos de funciones:
1) El volumen de un gas está determinado por la presión (a temperatura constante), esta relación viene dada por la ley de Boyle-Mariotte:
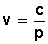
Donde v representa el volumen del gas en litros, p es la presión en atmósferas y c es una constante de proporcionalidad.
Se observa que al variar la presión a la que está sometido el gas varía el volumen; es decir, los valores del volumen dependen de los valores de la presión del gas y para cada valor de la presión existe un único valor del volumen.
2) El área A del círculo depende de la longitud de su radio r y está dada por la fórmula:
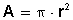
Si se conoce el valor del radio se puede conocer el valor del área del círculo.
3) Dada la función f(x) = 5x2 + 2
Encontrar el valor de la función para cuando x = 2.
Para calcular la imagen de un elemento bajo la función f, se reemplaza dicho elemento en el lugar de la variable, así para x = 2
F (2) = 5(2)2 + 2
F (2) = 22
Por lo tanto cuando x = 2, se tiene que f (2) = 22.
Ejemplo:
El precio de arrendar un auto es de 15 dólares más 0,20 de dólar por kilómetro recorrido.
a) Hallar la fórmula que expresa el costo del arriendo en función del número de los kilómetros recorridos.
b) ¿Cuánto hay que pagar si se han recorrido 50 kilómetros?
c) Si han cobrado 53 dólares ¿cuántos kilómetros se han recorrido?
Veamos:
a) Si llamamos x al número de kms recorridos, la fórmula de la función es f (x) = 15 + 0,2x.
b) x = 50 entonces
F (50) = 15 + 0,2 • 50 = 25
Hay que pagar 25 dólares.
c) f (x) = 53 entonces
15 + 0,2x = 53 entonces x = 190
Se han recorrido 190 km.
Álgebra de funciones
Suma, resta, multiplicación y división de funciones
Sean f y g dos funciones cualesquiera.
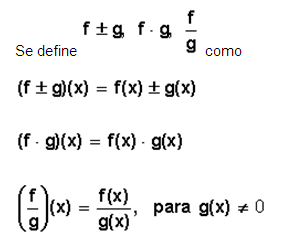
Ejemplos:
Suma de funciones
Sean las funciones

lunes, 1 de marzo de 2021
PARCIAL 01: PreCálculo - Desigualdades
Intervalos y su representación mediante desigualdades.
Una desigualdad es de una forma: 10 + 3 es mayor que 6. Se le representa por: Desigualdad: 10 + 3 > 6
Esta desigualdad se transforma en inecuación, cuando se introduce una incognita: Inecuacion: 10 + x > 6
En la recta numérica existe una relación de orden.
Cuando tenemos dos puntos de la recta numérica A y B, se pueden dar una de tres alternativas:
A es mayor que B A > B
A es igual a B A = B
A es menor que B A < B
Entonses por lo siguiente:
A > B v A=B
Destacamos que a < b es equivalente a b>a y así con otras expresiones, que se pueden “dar vuelta”.
Intervalos en los Reales (IR)
están entre otros dos reales “a” y “b” dados. En este caso x no puede ser ni “a” ni “b”.
Tipos de Intervalos:
Intervalo Abierto: Conjunto de números entre a y b, sin incluirlos, se simboliza por: ( )
Intervalo Cerrado: Conjunto de números entre a y b, incluidos ambos. Se simboliza po: [ ]
Intervalo Semiabierto por Derecha: Intervalo de puntos entre a y b, que incluye a “a” pero excluye a “b”. Simboliza: [ )
Intervalo Semiabierto por Izquierda: ( ]
Representación GRAFICA de intervalos:
[-3,6] -3< x < 6
(4,9) 4 < x < 9
lunes, 22 de febrero de 2021
PARCIAL 01: PreCálculo - Intervalos
¿Qué son los intervalos?
Un intervalo es un conjunto de números reales que se encuentra comprendido entre dos extremos, a y b. También puede llamarse subconjunto de la recta real.
Por ejemplo, los números que satisfagan una condición 1 ≤ x ≤ 5 ó [1;5] implican un intervalo que va desde el 1 hasta el 5, incluyendo a ambos.
Si se toma en cuenta la aplicación del intervalo para observar el comportamiento de una variable, se toma una serie de tiempo y se escoge un intervalo.
Clasificación de los intervalos
Existen 4 tipos de intervalos matemáticos, estos son: abierto, cerrado, semiabierto e infinito.
Intervalo abierto
Un intervalo abierto es aquel que no incluye los extremos entre los cuales está comprendido, pero sí todos los valores ubicados entre estos. Se representa mediante una expresión del tipo a < x < b ó (a;b).
Por ejemplo, si tenemos el intervalo abierto (1;5), tendremos el conjunto de números mayores a 1 y menores que 5. Sin incluir el 1 y el 5.

Representación en la recta real del intervalo abierto (a;b).
Intervalo cerrado
Un intervalo cerrado es aquel que incluye los extremos del intervalo y todos los valores comprendidos entre estos. Se representa con una expresión del tipo a ≤ x ≤ b ó [a;b].
Por ejemplo, si tenemos el intervalo cerrado [1;5], tendremos el conjunto de números mayores o iguales a 1 y menores o iguales a 5. Incluyendo el 1 y el 5.

Representación en la recta real del intervalo cerrado [a;b].
Intervalo semiabierto
Un intervalo semiabierto es aquel que incluye tan solo uno de los extremos de los valores que están entre ellos, de modo que el otro extremo queda excluido. Pueden estar incluidos o excluidos tanto el extremo derecho como el izquierdo.
Se representa con una expresión del tipo a ≤ x < b ó a < x ≤ b, lo que sería [a;b) ó (a;b].
Por ejemplo, si tenemos el intervalo semiabierto (1;5], tendremos un conjunto de números mayores a 1 y menores o iguales a 5. Sin incluir el 1 pero sí el 5.

Representación en la recta real del intervalo semiabierto [a;b).
Intervalo infinito
Un intervalo infinito es aquel que tiene un valor infinito en uno o ambos extremos. El extremo que posea el infinito será un extremo abierto. En caso de que ambos extremos sean infinitos, será la recta real.
Se representa con una expresión del tipo a ≤ x ó x ≤ a, lo que sería [a;∞) ó (-∞;a). Estos además pueden contener intervalos cerrados, como [a; ∞).
Por ejemplo, si tenemos el intervalo infinito [1;∞), tendremos un conjunto de números mayores o iguales a 1 en adelante.

Representación en la recta real del intervalo infinito [a;∞).
Ejemplos de intervalos
Para entender mejor el concepto de intervalos, veamos los siguientes ejemplos, junto con su clasificación y números comprendidos:
| Intervalo | Tipo | Comprende |
|---|---|---|
| (-4;6) | Abierto | Mayores que -4 y menores que 6. |
| (16;4) | Abierto | Mayores que 16 y menores que 4. |
| [5;6] | Cerrado | Mayores o iguales a 5 y menores o iguales a 6. |
| [10;14) | Semiabierto | Mayores o iguales a 10 y menores que 14. |
| (1;∞) | Infinito | Mayores que 1 en adelante. |
martes, 16 de febrero de 2021
PARCIAL 01: PreCálculo - Números reales
NÚMEROS REALES
Los números reales son cualquier número que corresponda a un punto en la recta real y pueden clasificarse en números naturales, enteros, racionales e irracionales.
En otras palabras, cualquier número real está comprendido entre menos infinito y más infinito y podemos representarlo en la recta real.
Los números reales son todos los números que encontramos más frecuentemente dado que los números complejos no se encuentran de manera accidental, sino que tienen que buscarse expresamente.
Los números reales se representan mediante la letra R ↓

Dominio de los números reales
Entonces, tal y como hemos dicho, los números reales son los números comprendidos entre los extremos infinitos. Es decir, no incluiremos estos infinitos en el conjunto.

Números reales en la recta real
Esta recta recibe el nombre de recta real dado que podemos representar en ella todos los números reales.

Esquema de los números reales
En este esquema podemos ver claramente que la organización de los números reales es similar al juego de muñecas rusas visto desde arriba o abajo.

Clasificación de los números reales
Tal y como hemos visto, los números reales pueden clasificarse entre números naturales, enteros, racionales e irracionales.
Los números naturales es el primer conjunto de números que aprendemos de pequeños. Este conjunto no tiene en cuenta el número cero (0) excepto que se especifique lo contrario (cero neutral).
Expresión:

Pista → Nos podemos acordar de los números naturales pensando en que son los números que usamos “naturalmente” para contar. Cuando contamos con la mano obviamos el cero, lo mismo para los números naturales.
Primeros elementos del conjunto de números naturales.

Los números enteros son todos los números naturales e incluyen el cero (0) y todos los números negativos.
Expresión:

Ejemplo de algunos de los elementos del conjunto de números enteros.

Pista: → Nos podemos acordar de los números enteros pensando en que son todos los números que usamos naturalmente para contar junto con sus opuestos e incluyendo el cero (0). A diferencia de los racionales, los números enteros representan “enteramente” su valor.
Los números racionales son las fracciones que pueden formarse a partir de los números enteros y naturales. Entendemos las fracciones como cocientes de números enteros.
Expresión:

Pista → Nos podemos acordar de los números racionales pensando en que siendo fracciones de números enteros, es “racional” que el resultado sea un número entero o un número decimal finito o semiperiódico.
Ejemplo de algunos de los elementos del conjunto de números racionales.

Los números irracionales son números decimales que no pueden expresarse ni de manera exacta ni de manera periódica.
Expresión:

Pista → Nos podemos acordar de los números irracionales pensando en que son todos los números que no encajan en las clasificaciones anteriores y que también pertenecen a la recta real.
Ejemplo de algunos elementos del conjunto de números irracionales.

Ejemplos de números reales
En el siguiente ejemplo sobre los números reales, comprueba que los siguientes números corresponden a punto en la recta real.
- Números naturales: 1,2,3,4…
- Números enteros: …,-4,-3,-2,-1, 0, 1, 2, 3, 4…
- Números racionales: cualquier fracción de números enteros.
- Números irracionales:

lunes, 15 de febrero de 2021
-
¿Qué son los intervalos? Un intervalo es un conjunto de números reales que se encuentra comprendido entre dos extremos, a y b. También pue...
-
Funciones Una función (f) es una relación entre un conjunto dado X (llamado dominio) y otro conjunto de elementos Y (llamado codominio) de...
-
NÚMEROS REALES Los números reales son cualquier número que corresponda a un punto en la recta real y pueden clasificarse en números natural...